[Data Structure] Hashing

Hashing

Hashing consists of 2 parts.

• A table (an array) of size m(T[0..m-1]).
• A hash function h, which maps a key into an index between 0 and m-1 inclusive.

Problem with Hashing

2 keys may have the same hash value - a collision.

To solve colilision, we need:

• A good hash function, that avoids collision.
• A collision resolution strategy.

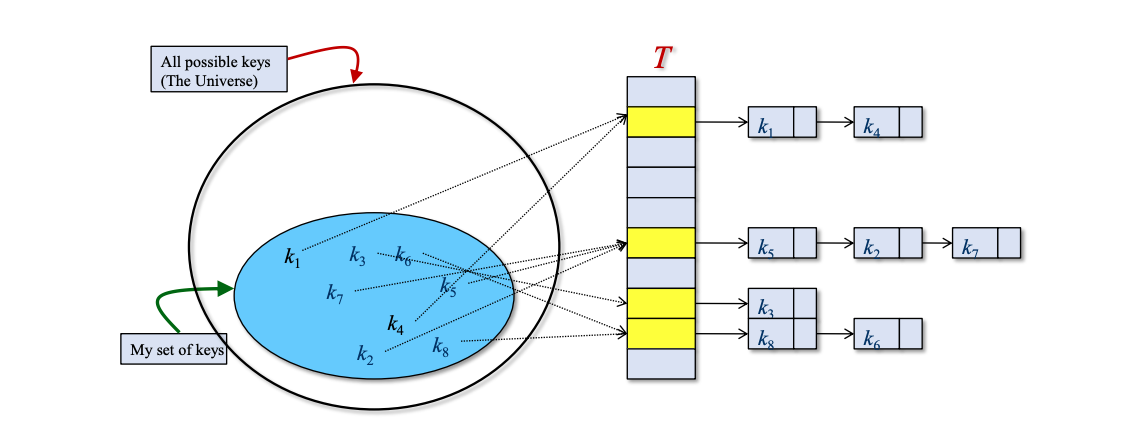
Chaining (Open Hashing)

Keep a linked list of all elements that have the same hash value.

Analysis of Chaining

• Insert takes constant time O(1).
• Delete takes constant time only if the pointer points to the node and the list is a doubly linked list, otherwise O(n).
• Searching takes O(n) at worst case when all the keys are mapped to the same slot.

Simple Uniform Hashing

The performance of hashing depends a lot on hash functions. The hash function should map the keys in the universe as uniformly as possible over the m slots. Moreover, the m slots should be given roughly the same number of elements.

This ideal hash function is known as simple uniform hashing.

The Division Method

In this hash function, k stands for key and m stands for table size.

With this hash function, the choice of m is very important.

• `h(k) = k mod m

A good hash function should use all the information provided by the keys.

Here are some rules to follow when choosing a good value for m:

1. m should not be a power of 2.
2. m should not be a power of 10, if application deals with decimal numbers.
3. Good value of m are prime numbers.

If it is difficult to choose prime numbers, pick m such that it has no prime numbers less than 20. (e.g., 23 x 31)

Multiplication Method

1. Pick a constant 0 < A < 1.
2. Take the fractional part of k x A.
3. Multiply the result by m.
4. Take the integer part of the result.
5. h(k) = int(frac(k x A) x m)

Note: A should be a irrational number.

Open Addressing (Closed Hashing)

Unlike chaining, all key-value pairs are stored in the hash table itself - element T[m].

There are 2 advantages compared to chaining.

1. It saves time in not doing memory allocation and de-allocation.
   • In chaining, collision results in the creation of a new node in a linked list, which requires dynamic memory allocation.
2. It saves space.
   • Pointers take space in chaining. (4 bytes each on a 32-bit machine)
   • If given same amount of memory, we can afford a larger number of spots under open addressing, resulting in fewer collision.

Probing

When inserting a key-value pair and collision occurs, alternative slots are tried until an empty slot is found.

This process is known as probing.

1. Searching
   • Follow the same probe sequence until the element is found, or an empty slot is encountered.
2. Insert
   • Follow the same probe sequence until empty slot or deleted slot is found.
3. Delete
   • Mark the deleted slot by storing the special value DELETED.

Load Factor

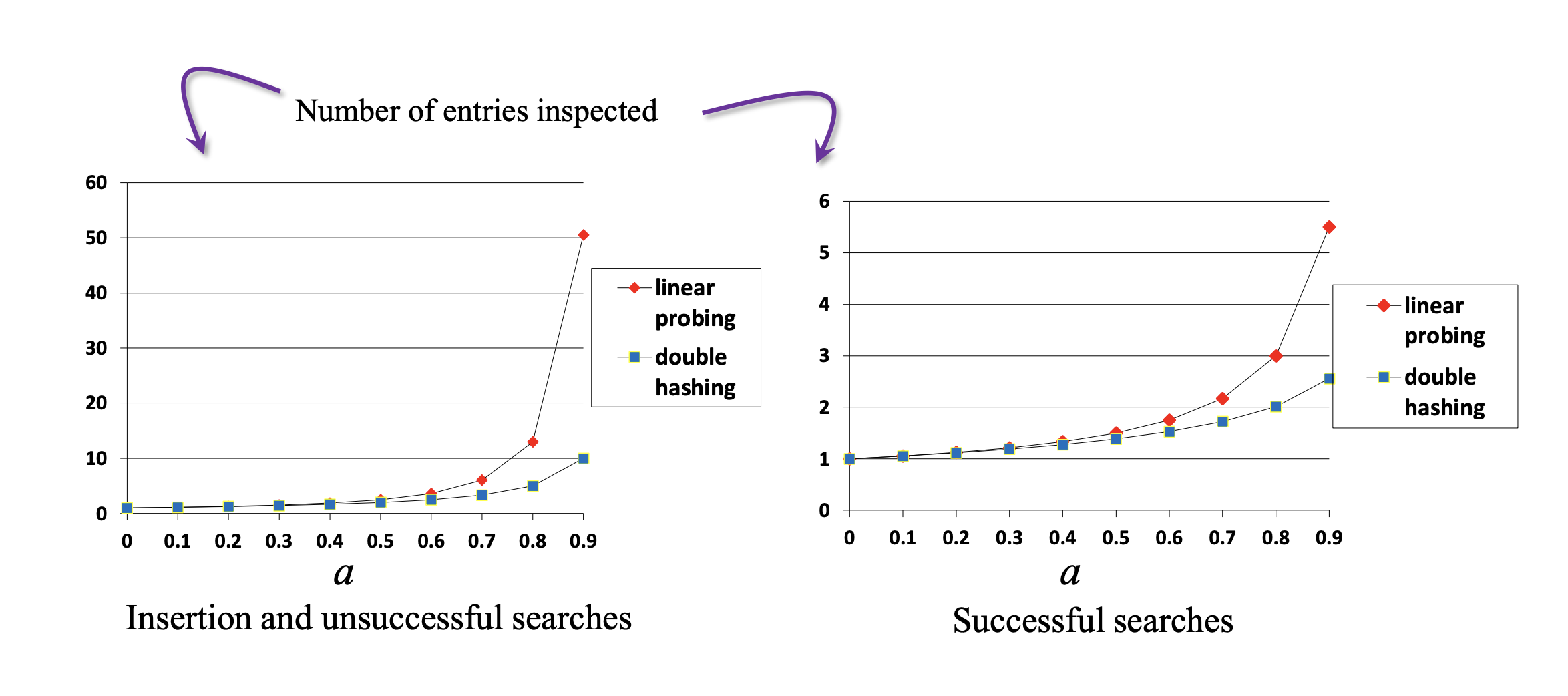
The load factor for open addressing should be below 0.5. This is because unlike chaining, open addressing has to store all its elements inside the table.

Probe Sequence

Depending on the increment function f(i), we have different types of probe sequences.

• h(k,i) = [h1(k) + f(i)] mod m

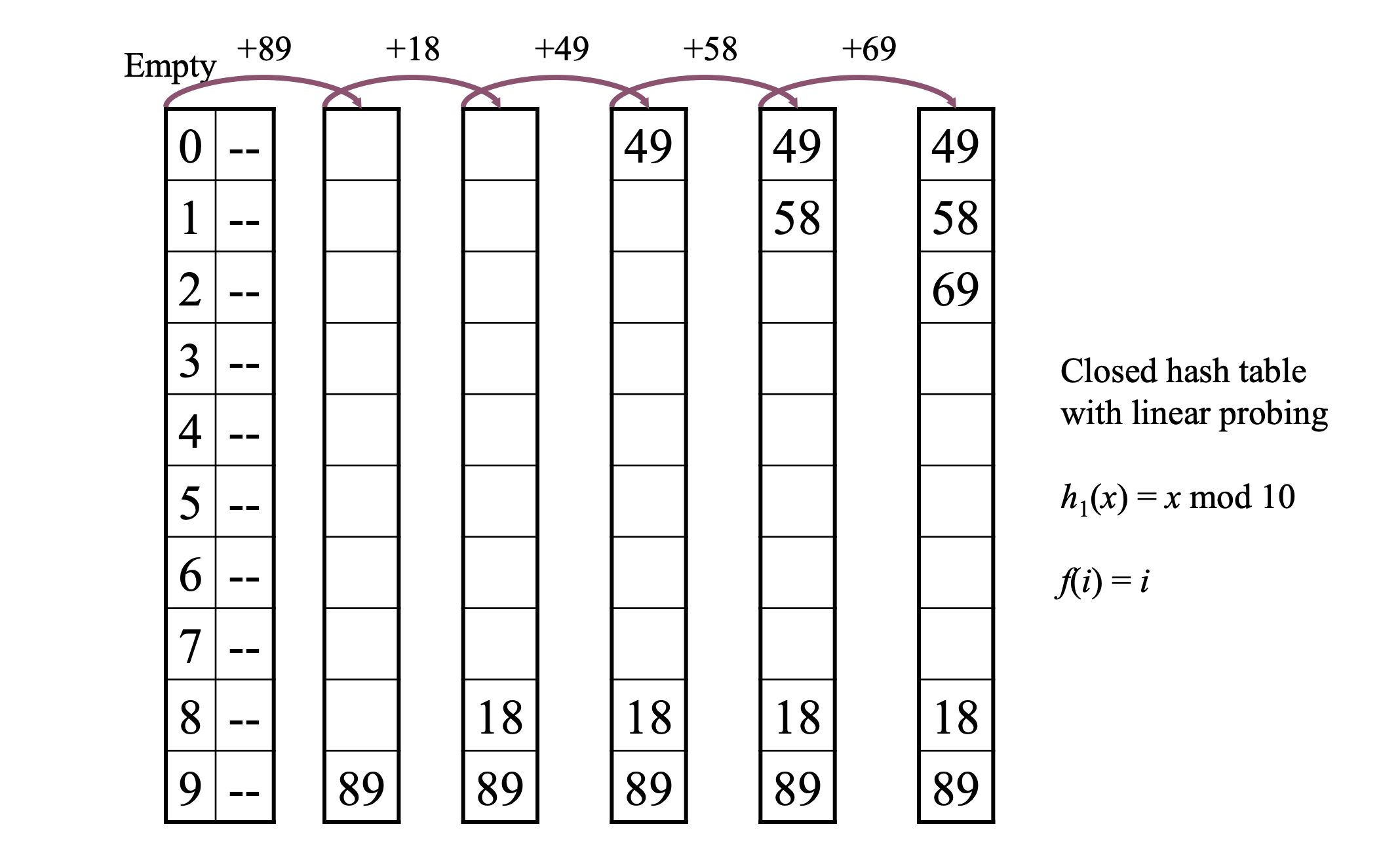
Linear Probing

f() is a linear funciton of i - f(i) = i. This means trying the slots in sequential order.

One problem is that linear probing causes primary clustering.

• Blocks of consecutively occupied slots are called clusters.
• The bigger the cluster is, the faster it grows.

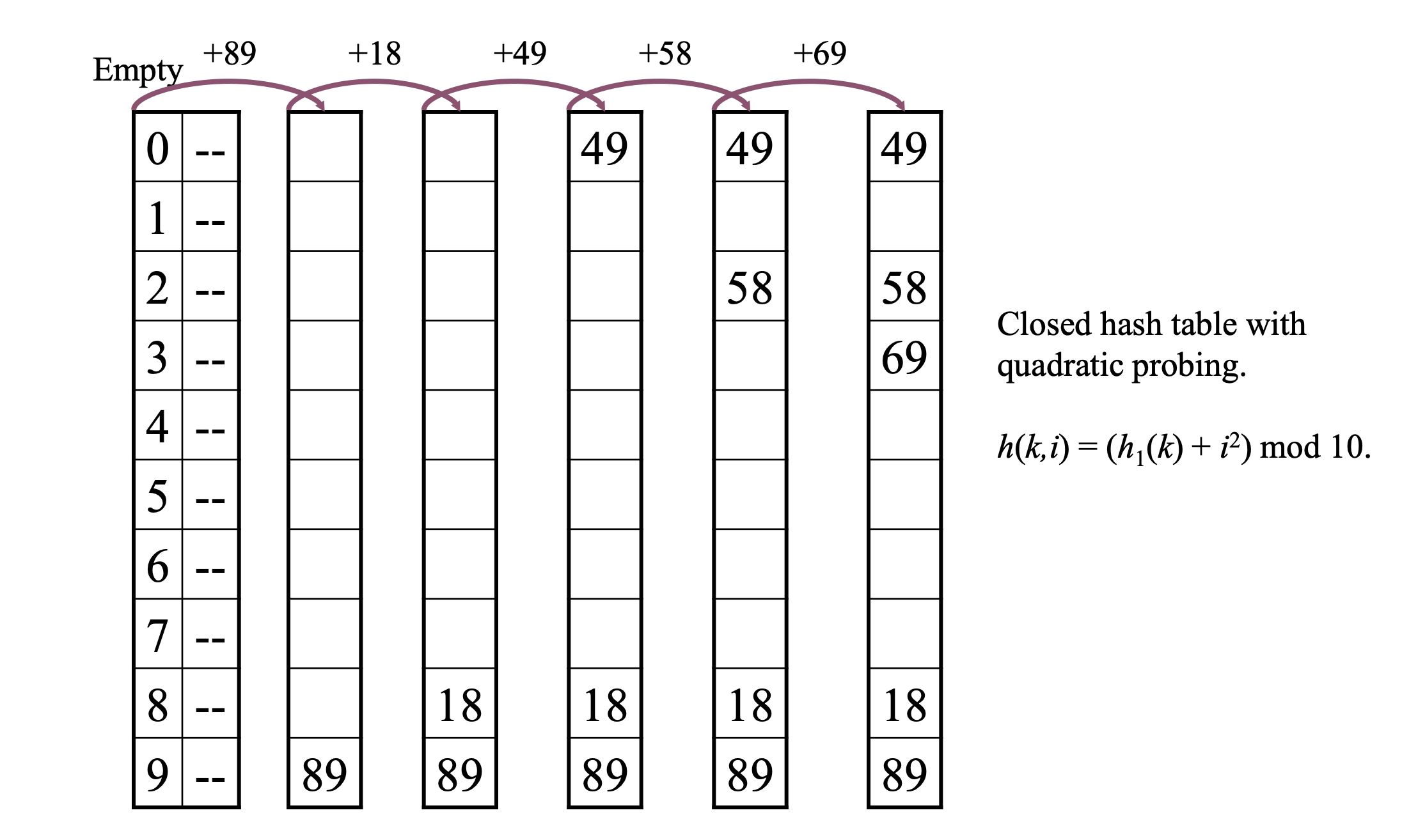
Quadratic Probing

Quadratic probing tries to solve the cluster problem by providing more probe sequences.

• h(k,i) = (h1(k) + i^2) mod m.

However, there are still problems with quadratic probing.

1. It may not span the whole table.
2. There are only m probe sequences - secondary clustering.

If you want to use quadratic probing, the table size must be a prime number and the table should never be full > half full.

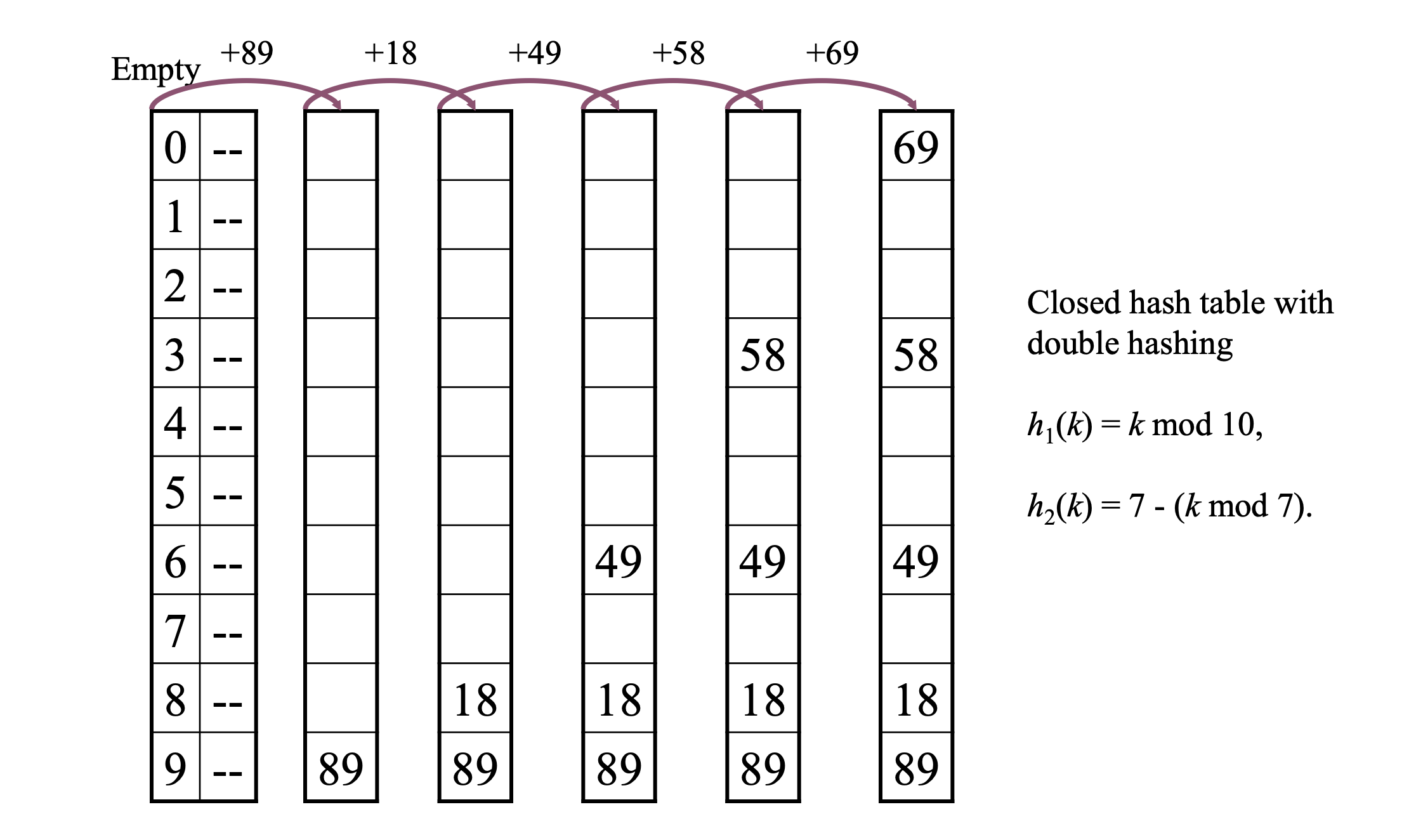
Double Hashing

Double hashing solves these cluster problems by utilizing 2 hash functions.

• h(k,i) = (h1(k) + i (h2(k))) mod m
• h1(k) determines the initial slot.
• h2(k) determines the increment.
  • it should never evaluate to 0.
  • it should be relatively prime to m (e.g., by setting m = a prime number and h2(k) to return values < m.)

It is very unlikely that two keys will have the same probe sequence because they would have to have the same hash value for the 2 hash functions.

Hence, clustering does not occur often.

Performance

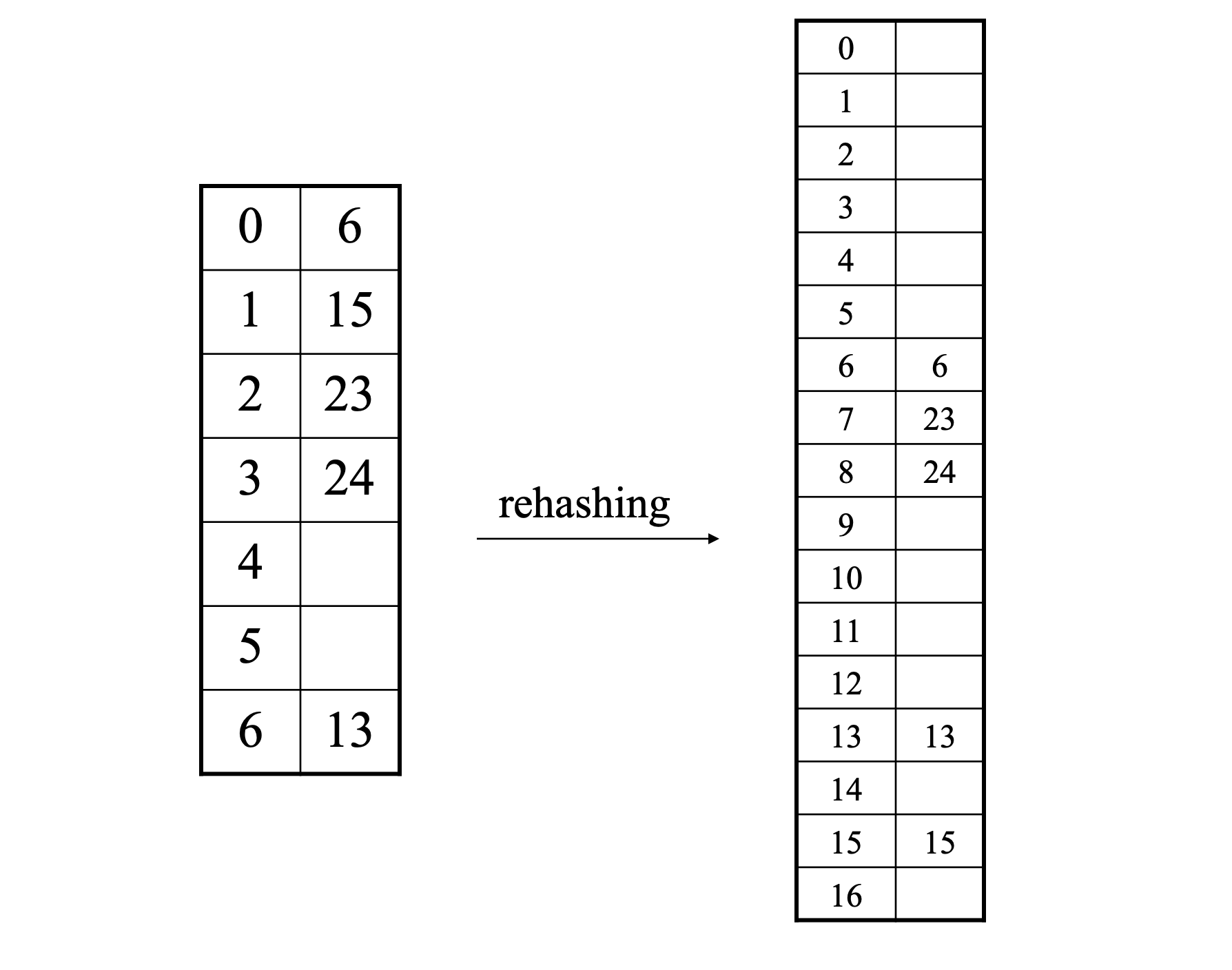
Rehashing

If the table gets to full a > 0.5, the operation will take more time.

The solution to this is building a larger hash table and rehashing the elements to a larger table.