[ALG/DP] Knapsnack Problem

1. What is Knapsnack Problem?

The Knapsack problem is a classic optimization problem in computer science where a set of items, each with a weight and a value, must be packed into a knapsack with a maximum weight capacity, such that the total value of the items packed is maximized.

2. Brute-Force Approach

The brute-force approach for solving the Knapsack problem involves generating all possible subsets of items and computing their total value and weight. The subset with the maximum value that satisfies the weight constraint is the solution to the problem. However, since the number of possible subsets of items is exponential in the number of items, this approach quickly becomes infeasible for large instances of the problem.

3. Dynamic Programming Approach

We can divide the problem into two cases.

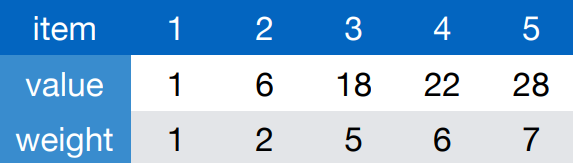
Subproblems: For any 1 ≤ i ≤ n and 1 ≤ w ≤ W, let N[i,w] be the maximum value of a subset of items 1 to i subject to capacity w.

W stands for total capacity / vn stands for value of item n / wn stands for weight of item w

• Case 1: the solution includes item n.

  • Item n contributes its value to the total value, but used up its weight from the total capacity.
  • It remains to choose a subset of items among the first n-1 items subject to a capacity of (total capacity - its weight).
  • N[n,W] = N[n-1,W-wn] + vn.
  • Remark: We do not need to consider the case when (its weight > total capacity)

• Case 2: the solution does not includes item n.

  • Item n does not contribute to the total value, so it does not use up the total capacity.
  • It remains to choose a subset of items among the first n-1 items subject to a capacity of total capacity.
  • N[n,W] = N[n-1,W].

In general, we can use max { N[i-1,w-wi] + vi, N[i-1,w] } to solve the problem.

PSEUDOCODE:

for (w=0; w<=W; w++)
  N(0,w) = 0;
for (i=1; i<=n; i++)
  for (w=0; w<=W; w++)
    N(i,w) = max { N[i-1,w-wi]+vi, N[i-1,w] }
return N(n,W);

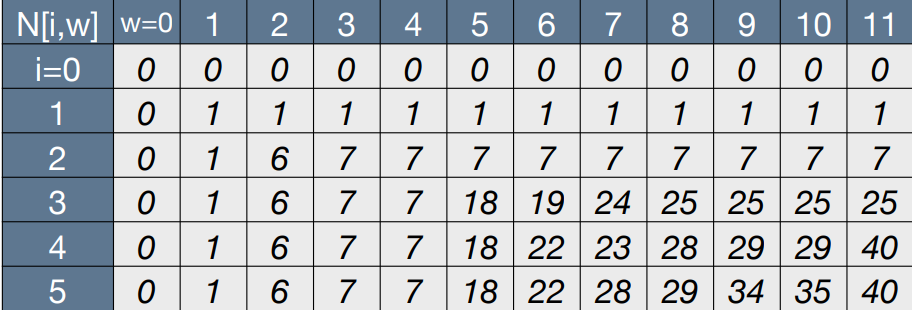
Sample Run: